Estudio cinético y termodinámico del pardeamiento no enzimático de zumos clarificados de pera

Kinetic and thermodynamic study of non-enzymatic browning of clarified pear juices

Raquel Ibarz a; Alfonso Garvín a; Albert Ibarz a

a Departamento de Tecnología, Ingeniería y Ciencia de Alimentos. Universidad de Lleida. Av. Rovira Roure, 191, 25198, Lleida, Catalunya. España.

* Autor corresponsal: A. Ibarz [ aibarz@tecal.udl.cat | https://orcid.org/0000-0003-0673-5174 ]

R. Ibarz [ raquel.ibarz@udl.cat | https://orcid.org/0000-0002-5559-0912 ]

A. Garvín [ garvin@tecal.udl.cat | https://orcid.org/0000-0003-2569-3432 ]

Resumen

En el presente trabajo se aplica la compensación cinética y termodinámica para evaluar las cinéticas de pardeamiento no enzimático de zumos clarificados de pera. Las constantes cinéticas se obtuvieron en un trabajo anterior para contenidos en sólidos solubles 47, 54, 63 y 70,5 °Brix y a temperaturas de 50, 60, 70, 80 y 90 °C. Para estas contantes cinéticas, las constantes de equilibrio se determinaron utilizando la ecuación de Eyring para cada contenido en sólidos solubles y cada temperatura. Las constantes cinéticas se ajustaron a la ecuación de Arrhenius y se comprobó que las parejas de valores estimados para lnK0 y la energía de activación siguen una tendencia lineal, lo que define que existe una compensación cinética, con una temperatura isocinética de 145,6 °C. Las constantes de equilibrio se ajustaron a la ecuación de Van't Hoff y el conjunto de los pares de valores estimados para la entalpía de activación y la entropía de activación siguieron una línea recta lo que da lugar a la compensación termodinámica, con una temperatura de isoequilibrio de 142,8 °C. Las temperaturas isocinéticas y de isoequilibrio resultaron muy similares. Se concluyó que el mecanismo es el mismo para los intervalos de contenido en sólidos solubles y temperatura estudiados. Dado que todas las temperaturas isocinéticas y de isoequilibrio fueron superiores a los valores de temperatura de trabajo, se concluyó que el control fue entálpico para todos los casos.

Palabras clave: compensación cinética; pardeamiento no enzimático; constantes cinéticas; temperatura de isoequilibrio.

Abstract

In the present work, kinetic and thermodynamic compensation is applied to evaluate the kinetics of non-enzymatic browning of clarified pear juices. The kinetic constants were obtained in previous work for soluble solids contents of 47, 54, 63 and 70.5 °Brix and at temperatures of 50, 60, 70, 80 and 90 °C. For these kinetic constants, the equilibrium constants were determined using Eyring's equation for each soluble solids content and temperature. The kinetic constants were fitted to the Arrhenius equation. The pairs of estimates for lnK0 and the activation energy follow a linear trend, defining a kinetic compensation, with an isokinetic temperature of 145.6 °C. The equilibrium constants were fitted to the Van't Hoff equation. The set of pairs of estimates for the activation enthalpy and activation entropy followed a straight line, giving rise to thermodynamic compensation, with an isoequilibrium temperature of 142.8 °C. As expected, the isokinetic and isoequilibrium temperatures were very similar. It was concluded that the mechanism is the same for the ranges of soluble solids content and temperature studied. Since all the isokinetic and isoequilibrium temperatures were higher than the working temperature values, it was concluded that the control was enthalpic for all cases.

Keywords: kinetic compensation; non-enzymatic browning; kinetic constants; isoequilibrium temperature.

1. Introducción

Las industrias que elaboran zumos clarificados de frutas los obtienen a través de un proceso industrial que comporta diferentes operaciones de procesado. El proceso se inicia con una etapa de lavado con el fin de eliminar residuos indeseables de la superficie de la fruta. A continuación, se trituran y la pasta obtenida se prensa, lo que permite obtener un zumo que contiene parte de fibra y pectinas, que se elimina en una etapa de ultrafiltración, para dar lugar a un zumo clarificado, cuyo contenido en sólidos solubles es el propio de la fruta (alrededor de 12 °Brix, dependiendo del tipo de fruta y estado de maduración). Este zumo clarificado se somete a una etapa de evaporación con el fin de eliminar parte del agua y obtener un zumo concentrado de aproximadamente 70 °Brix.

Durante el procesado, el zumo va variando su contenido en sólidos solubles y, además, se ve sometido a diferentes temperaturas, lo que puede dar lugar a pardeamientos de distinto grado, dependiendo de su contenido en sólidos solubles (Beveridge & Harrison, 1984). Dichos pardeamientos son provocados por la reacción de Maillard (pardeamiento no enzimático) entre azúcares reductores y los grupos amino libres (Cornwell & Wrolstad, 1981; Waller & Feather, 1983). Las altas temperaturas a las que se ve sometido el zumo en la etapa de evaporación favorecen la reacción de pardeamiento (Beveridge & Harrison, 1984).

Uno de los parámetros que definen la calidad del zumo es su color, por lo que el efecto de los pardeamientos no enzimáticos que oscurecen el zumo da lugar a un deterioro en su calidad. Por ello, se debe estudiar la variación del color de los zumos con distinto contenido en sólidos solubles y a las temperaturas que suelen darse en la etapa de evaporación. Con estos estudios se pueden obtener las cinéticas de reacción y, por tanto, las constantes cinéticas que permiten predecir el pardeamiento en las condiciones que se dan en los evaporadores (Labuza, 1985; Toribio & Lozano, 1986).

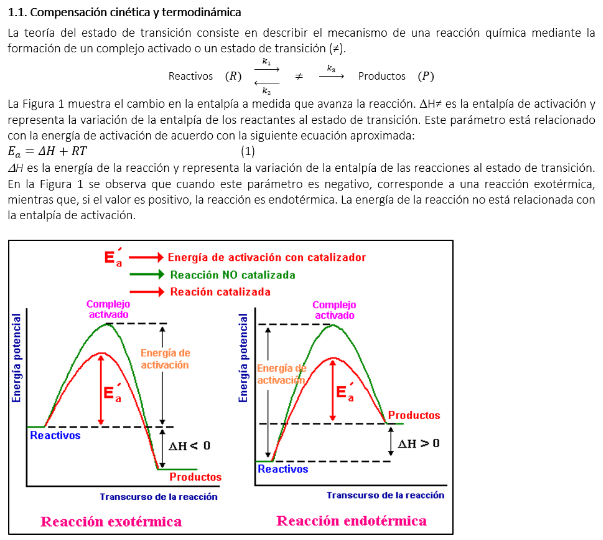
Figura 1. Esquema de la energía de activación (Ea) en reacciones endotérmicas y exotérmicas.

k3 es la constante cinética para un estado de transición y se puede definir por:

Cuando se estudia una reacción y la constante cinética se obtiene para varias temperaturas, la regresión lineal de la ecuación 9 linealizada permite obtener los valores de K0 y Ea y la regresión lineal de la ecuación 8 permite obtener H≠ y S≠. Si se estudia la misma reacción para varios valores de una variable experimental (por ejemplo, concentración de cualquier sustancia que no participa en el proceso) los cuatro parámetros estimados se pueden obtener para cada valor de la variable experimental.

La compensación cinética tiene lugar cuando al representar lnk0 frente a Ea se obtiene una relación lineal y la compensación entalpía-entropía tiene lugar cuando al representar H≠ frente a S≠ también se obtiene una relación lineal. No existe ninguna razón general que obliga a este tipo de relación lineal y que se puede encontrar en algunos casos, pero no en otros. En algunos casos se observa que la relación lineal es sólo una consecuencia de la propagación de errores experimentales entre dos parámetros estimados que se correlacionan (Krug, Hunter & Grieger, 1976a,b; Garvín, Ibarz & Ibarz, 2017).

1.1.3. Control de la reacción

Considerando la compensación cinética, a partir de la ecuación 10 se ha concluido que cuando la temperatura es la temperatura isocinética, la constante cinética no varía con la variable experimental (por ejemplo, contenido en sólidos solubles) debido a que la variación en el factor de frecuencia se compensa con la variación de la energía de activación.

donde n es el número de temperaturas utilizadas para estudiar la cinética de reacción.

La comparación de la temperatura isocinética con la media harmónica permite determinar si la compensación cinética y/o termodinámica es real o bien se atribuye a la propagación experimental de errores. Únicamente en el caso que el valor de Thm caiga fuera del intervalo de variación de la Tiso se puede hablar de que la compensación estudiada es real (Krug, Hunter & Grieger, 1976a; Garvín, Ibarz & Ibarz, 2017).

El objetivo del presente trabajo es evaluar la teoría de compensación cinética y termodinámica durante el pardeamiento de zumos clarificados de pera, utilizando los datos publicados previamente por Ibarz, Casero, Miguelsanz & Pagán (1989), considerando el contenido en sólidos solubles como la variable medioambiental.

2. Metodología

En este estudio se evalúa la teoría sobre la compensación cinética y termodinámica de los datos publicados por Ibarz, Casero, Miguelsanz & Pagán (1989), quienes estudiaron el efecto de la temperatura sobre la cinética de pardeamiento no enzimático de zumos clarificados de pera con diferente contenido en sólidos solubles. Estos autores evaluaron el pardeamiento sobre zumos de 47, 54, 63 y 70,5 °Brix a las temperaturas de 50, 60, 70, 80 y 90 °C. La variación de la absorbancia de los zumos a 420 nm, para todas las temperaturas y contenidos en sólidos solubles se ajustaron a una cinética de primer orden.

Se han tomado los datos de las constantes cinéticas de primer orden del estudio de Ibarz et al. (1989). En dicho artículo se muestran con detalle los materiales y métodos utilizados para obtener estas contantes cinéticas. Todas las regresiones utilizadas en el presente artículo se han obtenido a partir del paquete estadístico STATGRAPHICS Centurion XVI (Statistical Graphics Corp., Warrenton, VA, USA), utilizando un nivel de probabilidad el 95%.

3. Resultados y discusión

En la tabla 1 se muestran los datos de las constantes cinéticas de primer orden del estudio de Ibarz et al. (1989) que se han adecuado a las cifras significativas que marca el intervalo de variación de este parámetro. Todos los coeficientes de determinación están comprendidos entre los valores 0,9510 y 0,9990. En la tabla se observa que las constantes cinéticas aumentan con el contenido en sólidos solubles y la temperatura de tratamiento. Para un determinado contenido en °Brix, el valor de la constante cinética aumenta con la temperatura. Para una determinada temperatura el valor de la constante cinética aumenta con el contenido en sólidos solubles.

Tabla 1

Constantes cinéticas de primer orden del pardeamiento no enzimático en zumos clarificados y despectinizados de pera a diferentes temperaturas y distinto contenido en sólidos solubles (Ibarz et al., 1989)

3.1. Compensación cinética

Para cuantificar el efecto que la temperatura ejerce sobre la constante cinética de pardeamiento no enzimático, para cada contenido en sólidos solubles, los datos de la Tabla 1 se han ajustado a la ecuación de Arrhenius (Ec. 9), obteniendo que tanto el ajuste como los valores estimados de los parámetros de este ajuste son significativos a un nivel de probabilidad del 95%. En la Tabla 2 se muestran los resultados de los ajustes obtenidos, donde se observa que al disminuir el contenido en sólidos solubles los valores de las energías de activación aumentan.

Tabla 2

Valores de los parámetros de la ecuación de Arrhenius (Ec. 9) para los distintos contenidos en sólidos solubles estudiados

(*) K0 en min-1

Al objeto de estudiar si existe compensación cinética, los valores de ln K0 y Ea deberían mostrar una tendencia lineal, es decir, la compensación tiene lugar cuando al representar el logaritmo neperiano del factor de frecuencia (ln K0) frente a la energía de activación (Ea) da una línea recta (Garvín, Ibarz & Ibarz, 2017). La ordenada en el origen a sería el valor del logaritmo neperiano de la constante (a = ln kiso) a la temperatura isocinética, mientras que de la pendiente b es posible obtener el valor de dicha temperatura isocinética (Tiso) utilizando la ecuación 13.

Tomando los datos presentados en la Tabla 2 se puede construir la Figura 2, en la que se han graficado los valores de ln K0 frente a los valores de la energía de activación (Ea) para los ajustes con diferente contenido en sólidos solubles. Los datos de la variación de ln K0 con la energía de activación para las diferentes muestras con distinto contenido en sólidos solubles se han ajustado a una línea recta, obteniendo la siguiente ecuación:

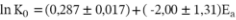
R2 = 0,9928.

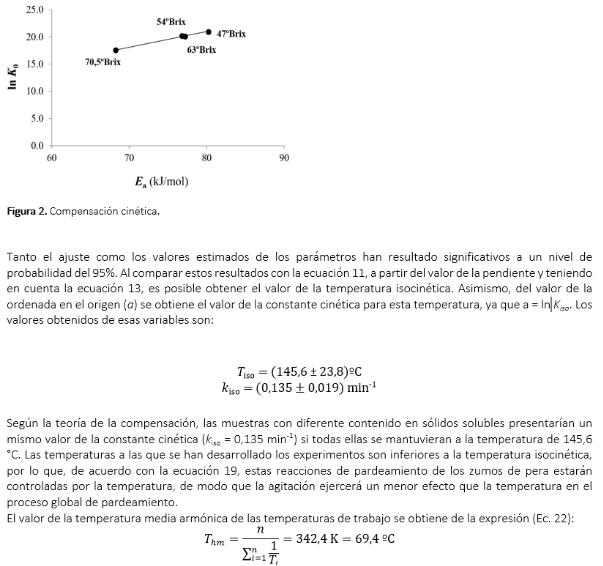
Se observa que el valor de la temperatura media armónica cae fuera del intervalo de variación de la temperatura isocinética. Por lo tanto, se puede admitir que existe una compensación real (Krug, Hunter & Grieger, 1976a; Garvín, Ibarz & Ibarz, 2017).

En la Figura 3 se muestran los valores de las constantes cinéticas mostrados en la Tabla 1 así como las curvas resultantes del ajuste de la variación de dichas constantes con la temperatura. Los valores de estas constantes están referidas al eje principal de ordenadas de la izquierda, mientras que en el eje secundario de la derecha aparecen las curvas del ajuste para el intervalo de temperaturas que incluye el punto isocinético. Se puede observar que en las proximidades del punto isocinético (145,6; 0,135) todas las curvas del ajuste prácticamente coinciden tendiendo hacia este punto. En este punto el valor de la constante cinética será el mismo para todas las muestras indepen-dientemente de su contenido en sólidos solubles. Además, como la temperatura isocinética es una consecuencia matemática, sólo se puede comprobar experimentalmente cuando el mecanismo de reacción y el estado físico se mantienen iguales entre el intervalo de temperaturas de trabajo y a la tempera-tura isocinética.

Como el valor de la temperatura isocinética es 145,6 °C es imposible llevar a cabo la comprobación experimental de este punto isocinético.

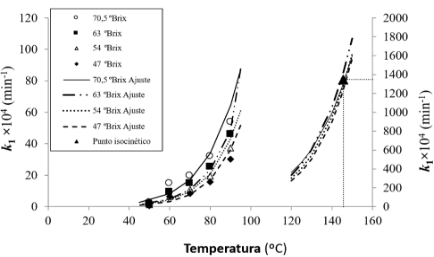
Figura 3. Constantes cinéticas de pardeamiento para todas las temperaturas estudiadas a todos los contenidos en sólidos solubles (eje de la izquierda) y las tendencias teóricas (eje de la derecha) con el punto isocinético.

3.3. Compensación Termodinámica

A partir de las contantes cinéticas de pardeamiento mostradas en la Tabla 1 es posible calcular los valores de las entalpías y entropías del estado de transición. Al representar los valores de ln [(k1 hp)/(kb T)] frente a la inversa de la temperatura absoluta (1/T) se obtiene una recta (Ec. 8), a partir de la cual se obtiene una ordenada en el origen, de cuyo valor se puede calcular la entropía del estado de transición (ΔS#). Del valor de la pendiente es posible obtener el correspondiente valor de la variación de entalpía del estado de transición (ΔH#). Tanto los ajustes como los valores estimados de los parámetros han resultado significativos a un nivel de probabilidad del 95%. En la Tabla 3 se muestran los valores obtenidos en los ajustes.

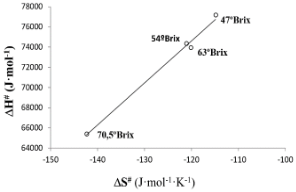
Figura 4. Compensación termodinámica.

Además, a partir del valor de 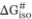a través de la ecuación 4 se obtiene el valor de la constante de equilibrio para este punto de isoequilibrio (Kiso# = 2,28×10-16). Tal como era de esperar, la temperatura isocinética y de isoequilibrio son realmente similares. Del mismo modo que con la temperatura isocinética, la temperatura media armónica (Thm = 69,4 °C) cae fuera del intervalo de variación de la temperatura de isoequilibrio. Por lo tanto, se puede admitir que existe una compensación real (Krug, Hunter & Grieger, 1976a; Garvín, Ibarz & Ibarz, 2017). Asimismo, como las temperaturas utilizadas en los experimentos son inferiores a la de isoequilibrio, se concluye que estas reacciones de pardeamiento de los zumos de pera estarán controladas por la temperatura y que la agitación ejercerá un efecto en el proceso de pardeamiento menor al cambio en la temperatura.

A partir de la ecuación de Van't Hoff (Ec. 4 y 5) y con los valores de la variación de entalpía (ΔH#) y entropía (ΔS#) mostrados en la Tabla 3 es posible obtener los valores de la constante de equilibrio (K#eq) de cada muestra con distinto contenido en sólidos solubles y cada temperatura de trabajo. En la Figura 5 se mues-tran los valores de las constantes de equilibrio para las diferentes muestras, así como el punto de isoequilibrio. En esta figura, los valores de K#eq se muestran en el eje principal de ordenadas de la izquierda y en el eje secundario de la derecha se muestran las curvas del ajuste para el intervalo de temperaturas que incluye el punto de isoequilibrio (142,8; 2,28×10-16).

Se observa que todas las curvas tienden a coincidir (aproximadamente) al valor de isoequilibrio. A lo que se presentaba con la compensación cinética, en este caso la temperatura de isoequilibrio es una consecuencia matemática y únicamente se puede comprobar experimentalmente cuando el mecanismo de reacción y el estado físico continúa siendo el mismo para el intervalo de las temperaturas de trabajo y la temperatura de isoequilibrio. Como el valor de la temperatura isoequilibrio es de 142,8 °C es imposible llevar a cabo la comprobación experimental de este punto isoequilibrio.

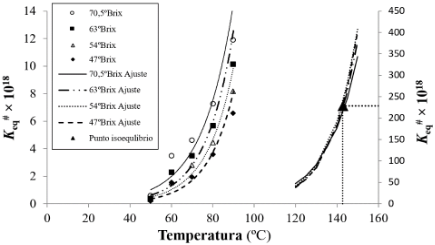
Figura 5. Constantes de equilibrio para el estado de equilibrio involucrado en el mecanismo del estado de transición para todas las temperaturas estudiadas a todos los contenidos en sólidos solubles (eje de la izquierda) y las tendencias del ajuste (eje de la derecha) con el punto de isoequilibrio.

4. Conclusiones

Los pardeamientos no enzimáticos provocados por la temperatura en zumos de pera clarificados con distinto contenido en sólidos solubles se describen mediante una cinética de primer orden. El mecanismo de este tipo de reacciones se supone que se desarrolla a través de una etapa con la formación de un complejo activado o estado de transición (#) que posteriormente puede dar lugar a la formación de productos de reacción o retorno hacia los reactantes.

Se ha comprobado que este proceso de pardeamiento sigue las relaciones lineales correspondientes a las compensaciones cinética y termodinámica, con valores similares de las temperaturas isocinética (145,6 °C) y de isoequilibrio (142,8 °C). Puesto que el valor de la temperatura media armónica (Thm = 69,4 °C) está localizado fuera del intervalo de confianza de las temperaturas isocinética y de isoequilibrio, se descartó que la compensación pudiera ser causada por la propagación de los errores experimentales. Por lo tanto, se asume que estas cinéticas de pardeamiento no enzimático mantienen el mismo mecanismo de reacción para todas las temperaturas de trabajo y contenidos en sólidos solubles, estando controlado entálpicamente y las constantes cinéticas y de equilibrio en función de los valores de la concentración.

Referencias bibliográficas

Beveridge, T., & Harrison, J. E. (1984). Nonenzymatic browning in pear juice concentrate at elevated temperatures. Journal Food Science, 49, 1335-1340.

Cornwell, C. J., & Wrolstrad, R. E. (1981). Causes of browning in pear juice concentrate at elevated temperatures. Journal Food Science, 46, 515-518.

Garvín, A., Ibarz, R., & Ibarz, A. (2017). Kinetic and thermodynamic compensation. A current and practical review for foods. Food Research International, 96, 132-153.

Ibarz, A., Casero, T., Miguelsanz, R., & Pagán, J. (1989). Efecto de la temperatura en la cinética de pardeamiento no enzimático en zumos clarificados de pera con diferente contenido en sólidos solubles. Revista de Agroquímica y. Tecnología de Alimentos, 29(4), 530-537.

Krug, R. R., Hunter, W. G. & Grieger, R. A. (1976a). Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of Van’t Hoff and Arrhenius data. The Journal of Physical Chemistry, 80(21), 2335-2341.

Krug, R. R., Hunter, W. G., & Grieger, R. A. (1976b). Enthalpy-entropy compensation: Separation of the chemical from the statistical effect. Journal of Physical Chemistry, 80(21), 2341–2351.

Labuza, T. P. (1985). An integrated approach of food chemistry: Illustrative cases. In: Food Chemistry. ed. 2, O.R. Fennema, Ed., Marcel Dekker, New York, 913–938.

Leffler, J. E. (1955). The enthalpy-entropy relationship and its implications for organic chemistry. Journal of Organic Chemistry, 20(9), 1202–1231.

Özilgen, M., & Bayindirli, L. (1992). Frequency factor-activation energy compensation relations for viscosity of the fruit juices. Journal of Food Engineering, 17, 143-151.

Toribio, J. L., & Lozano, J. E. (1986). Heat induced Browning of clarified Apple juice at high temperatures. Journal Food Science, 51(1), 172-175.

Waller, G. R., & Feather, M. S. (1983). Maillard Reaction in Foods and Nutrition. ACS Symposium series 215. Am. Chem. Soc. Washington.